数据结构与算法
数据结构和算法,是大厂前端面试的“拦路虎”。为何要考察呢?如果在短时间之内快速判断一个工程师是否优秀?辨别优秀工程师从鉴别成本和成功率的方面考虑,它的算法不一定是很厉害的,但是是过关的,所以考察算法是最合理的方式 —— 这是业界多年的经验积累。
另外现在前端的工作范围越来越广,前端可以做服务端、客户端、PC端大型业务系统等,越来越广那么要求越来越高。
考察的重点:
- 算法的时间复杂度和空间复杂度
- 三大算法思维:贪心,二分,动态规划
- 常见数据结构
什么是复杂度
复杂度是程序执行时的计算量和内存空间(和代码是否简介无关),它是一个数量级(方便记忆、推广),不是数字。复杂度一般是针对一个具体的算法,这个算法可能是一个函数,而非一个完整的系统。
数量级用O()来表示,比如:O(1)一次就够(数量级),O(n)和传输的数据量一样(数量级),O(n^2)数据量的平方(数量级),O(logn)数据量的对数(数量级),O(nlogn)数据量数据量的对数(数量级),其中logn可以理解为一个二分的循环算法。
时间复杂度
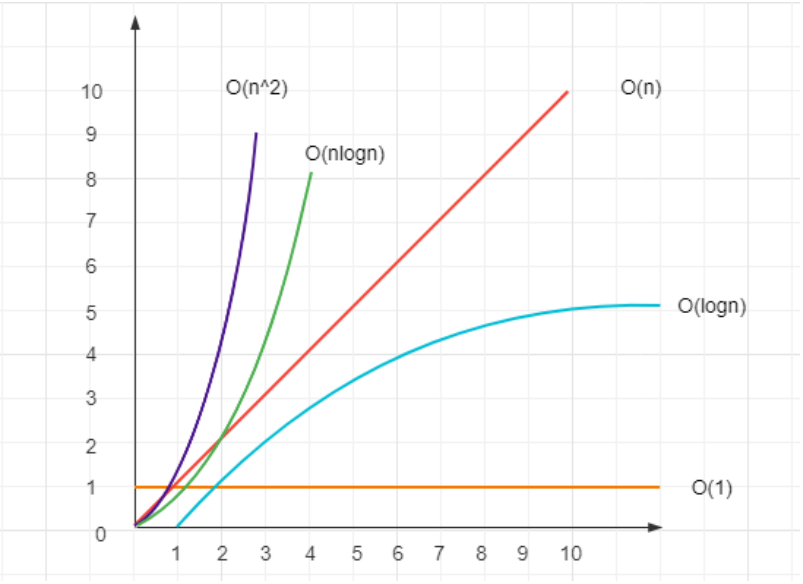
- O(1):代码就是平铺直叙的执行,没有任何循环。
- O(logn):有循环,但其中使用了二分法,例如:二分查找算法,二分法是非常重要的算法思维,它可以极大的减少复杂度,而且计算量越大、减少的越明显。可以看看本文上面的图。
- O(n):普通的循环。
- O(n*logn):嵌套循环,一层是普通循环,一层有二分算法。例如:快速排序算法。
- O(n^2):两个普通循环的嵌套,例如常见的冒泡排序。
空间复杂度
空间复杂度指的是程序运行所需要的内存空间,在前端领域是重时间轻空间,因为运行在浏览器中基本上比较强大足够用。
- O(1)有限的、可数的空间(数量级)
- O(n)和输入的数据量相同的空间(数量级)
程序员必须掌握算法复杂度,如果你没有复杂度的概念和敏感度,写程序时非常危险的。例如,代码功能测试正常,但数量大了,程序就崩溃。对于前端而言,尤其是时间复杂度。
为什么要学习数据结构与算法
当我们通过框架或工具来开发的时候,其实我们对框架或工具的影响度较低,就算我们可以通过配置进行内部的处理,但是核心还是由库和框架决定的。那么我们希望优化我们的程序,那么从哪方面入手呢?这时候我们可以利用数据处理操作优化功能,这里就需要使用数据结构和算法的相关内容。
那么我们常说数据结构+算法=程序,数据结构我们在开发中比较常用,例如数组,算法常用的像排序算法。利用特定的数据结构和算法对我们的程序书写的复杂度会有一个简化,让代码化繁为简,其次也能提升代码程序的性能,另外也能提升面试通过率。
栈
栈是一种遵从后进先出原则的有序集合,添加新元素的一端称为栈顶,另一端称为栈底。操作栈的元素时,只能从栈顶操作(添加、移除或取值)。 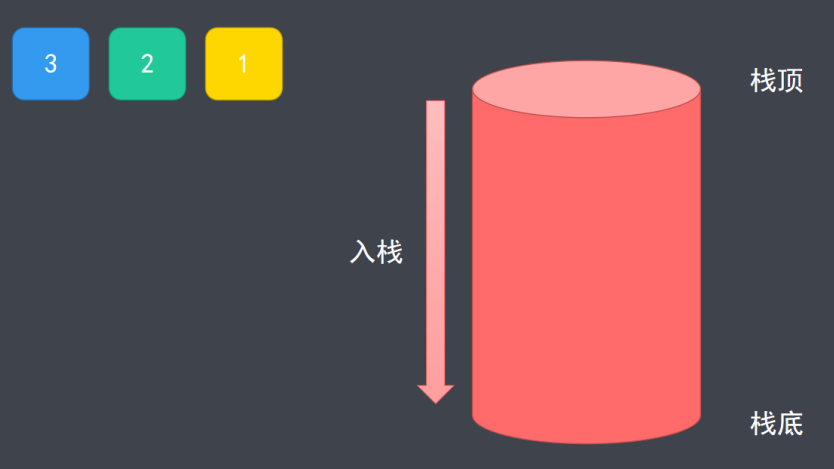

栈需要实现以下功能:
- push()入栈方法
- pop()出栈方法
- top()获取栈顶值
- size()获取栈的元素个数
- clear()清空栈
class Stach{
constructor(){
//存储栈的数据
this.data = [];
//记录栈的数据个数(相当于数组的Length)
this.count = 0;
}
//push()入栈方法
push(item){
//方式1:数组方法push添加
//this.data.push(item)
//方式2:利用数组长度
//this.data[this.data.length] = item
//方式3:计数方式
this.data[this.count] = item;
//入栈后,count自增
this.count++;
}
//pop()出栈方法
pop(){
//出栈的前提是栈中存在元素,应先行检测
if(this.isEmpty()){
console.log('栈为空!');
return;
}
//移除栈顶数据
//方式1:数组方法pop移除
//return this.data.pop();
//方式2:计数方式
const temp = this.data[this.count -1];
delete this.data[--this.count];
return temp;
}
//检测栈是否为空
isEmpty(){
return this.count === 0;
}
//top()用来获取栈顶值
top(){
if(this.isEmpty()){
console.log('栈为空');
return
}
return this.data[this.count - 1];
}
//size()获取元素个数
size(){
return this.count;
}
//clear()清空栈
clear(){
this.data = [];
this.count = 0;
}
}LeetCode精选题目
包含min函数的栈
队列
队列是一种遵循先进先出原则的有序集合,添加新元素的一端称为队尾,另一端称为队首。


队列需要实现以下功能:
- enqueue()入队方法
- dequeue()出队方法
- top()获取队首值
- size()获取队列元素个数
- clear()清空队列
基于数组实现队列
class Queue{
constructor(){
//用于存储队列数据
this.queue = [];
this.count = 0;
}
//入队方法
enqueue(item){
this.queue[this.count++] = item;
}
//出队方法
dequeue(){
if(this.isEmpty()){
return;
}
//删除queue的第一个元素
//delete this.queue[0]
//利用shift移除数组第一个元素
this.count--;
return this.queue.shift();
}
isEmpty(){
return this.count === 0;
}
//获取队首元素值
top(){
if(this.isEmpty()){
return;
}
return this.queue[0];
}
size(){
return this.count;
}
clear(){
this.queue = [];
}
}基于对象实现队列
class queue{
constructor(){
this.queue = {};
this.count = 0;
//用于记录队首的键
this.head = 0;
}
//入队方法
enqueue(){
this.queue[this.count++] = item;
}
//出队方法
dequeue(){
if(this.isEmpty()){
return;
}
const headData = this.queue[this.head];
delete this.queue[this.head];
this.head++;
this.count--;
return headData;
}
isEmpty(){
return this.count === 0;
}
clear(){
this.queue = {};
this.count = 0;
this.head = 0;
}
}链表
链表是一种有序的数据结构,链表中的每个部分称为节点,链表在内存中不必是连续的空间,它的优点是添加与删除不会导致其他元素位移,缺点是无法根据索引快速定位元素。链表与栈队列的区别是链表可以从首尾以及中间位置进行数据操作。那么链表可以从首、尾、中间进行数据存取,那为什么不直接使用数组呢?大家都知道数组在内存中占用一段连续的空间,而添加、移除会导致后续元素位移,性能开销大。 
由于这种原因,那么有没有更好的存储方式能够去优化数组的相关功能,例如我们对一个数组经常添加移除。这时就需要链表来去优化。
链表的实现:
- 节点类:value存储当前节点的数据、next存储下一个节点的指针
- 链表类:addAtTail尾部添加节点、addAtHead头部添加节点、addAtIndex指定位置添加节点、get获取节点、removeAtIndex删除指定节点
//节点类
class LinkedNode{
constructor(value){
this.value = value
//用于存储下一个节点的引用
this.next = null
}
}
//链表类
class LinkedList{
constructor(){
this.count = 0
this.head = null
}
//添加节点(尾)
addAtTail(value){
//创建新节点
const node = new LinkedNode(value)
//检测链表是否存在数据
if(this.count === 0){
this.head = node
this.count++
}else{
//找到链表尾部节点,将最后一个节点的next设置为node
let cur = this.head
while(cur.next!=null){
cur = cur.next
}
cur.next = node
this.count++
}
}
}树
树形结构是一种非线性数据结构,树中的每个部分称为结点,结点间存在分支结构与层次关系。 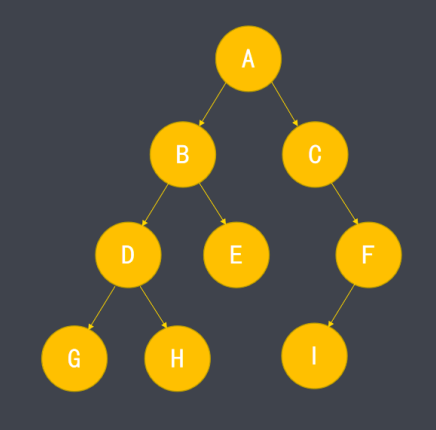
树和栈、队列、链表等结构不太相似,栈、队列等结构都属于线性结构,而树属于非线性结构。
树形结构我们在开发中常见的就是DOM树 
每个树形结构都有一个根结点例如A结点,根据结点之间的关系,也存在父结点、子结点、兄弟结点的概念。 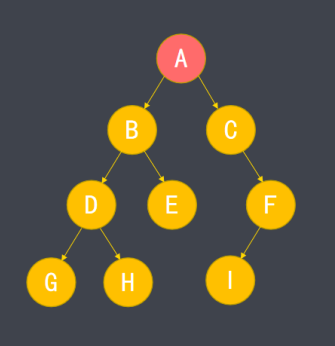
不含子结点的结点称为叶结点,例如G、H、I。 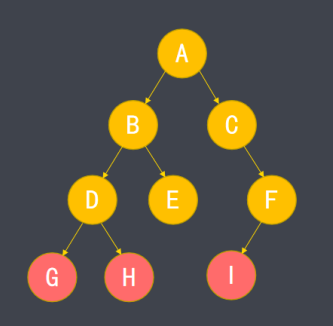
子树是对某个结点与其后代结点的整体称呼,例如D、G、H形成了一个子树 
由于存在父子关系,树中的结点形成多级结构,称为层级。根节点层级为1,向下依次递增。树中最深结点的层级称为树的高度。 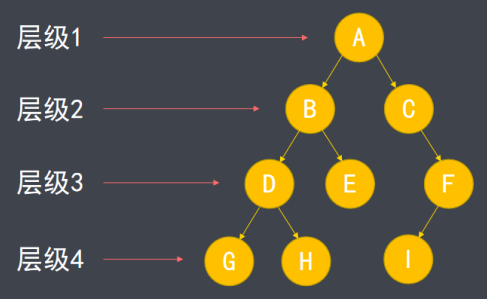
二叉树
二叉树是树形结构中的一种,二叉树中的每个结点最多只能存再2个子结点。二叉树中的结点有更明确的称呼为左子结点、右子结点。例如A有两个子结点,左子结点B和右子结点C。B之后延伸的称为左子树,C之后延伸的称为右子树

除了普通二叉树外,还存在一些特殊形式的二叉树。如下图,二叉树的每层结点都达到最大值,称为满二叉树。 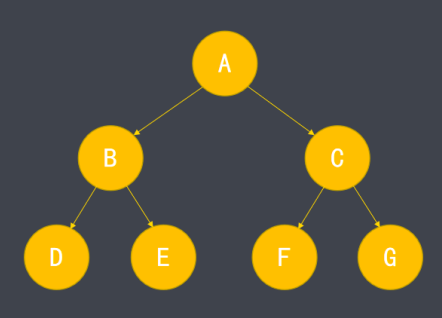
二叉树的除最后一层外,每层结点都达到最大值,且最后一层结点都位于左侧,这种形式称为完成二叉树。满二叉树也属于完成二叉树。 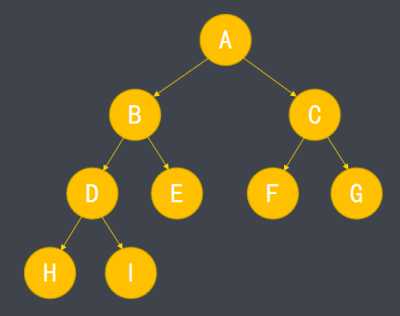
二叉树的存储形式
由于完全二叉树的结构连续,有迹可循,可采用顺序存储方式。如按照从左往右,从上到下的顺序将结点存储在数组中。
普通二叉树由于结构不规则,不适合使用顺序存储,为了记录结点间的关系,可使用链式存储方式。每个结点通过value表示值,left、right表示左右子结点。
排序算法复杂度
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空闲复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | In-place | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | In-place | 不稳定 |
| 插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | In-place | 稳定 |
| 希尔排序 | O(n log n) | O(n log^2 n) | O(n log^2 n) | O(1) | In-place | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | Out-place | 稳定 |
| 快速排序 | O(n log n) | O(n log n) | O(n^2) | O(logn) | In-place | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | In-place | 不稳定 |
| 计数排序 | O(n + K) | O(n + K) | O(n + K) | O(k) | Out-place | 稳定 |
| 桶排序 | O(n + k) | O(n + K) | O(n^2) | O(n + K) | Out-place | 稳定 |
| 基数排序 | O(n x k) | O(n x k) | O(n x k) | O(n + K) | Out-place | 稳定 |
判断字符串是否括号匹配
一个字符串s可能包含{}()[]三种括号,判断s是否是括号匹配的,如(a{b}c)匹配,而{a(b或{a(b}c)就不匹配。
这个题考察的就是栈,它是非常基础的数据结构,它是先进后出的数据结构。很多人会问栈和数组有什么区别?栈是逻辑结构,理论模型,不管如何实现,不受任何语言的限制。数据是物理结构,真实的功能实现,受限于编程语言。数组可以实现栈。
这道题的思路就是遇到左括号{([就压栈,遇到有括号})]就判断栈顶,匹配则出栈。最后判断length是否等于0。
/**
* 判断左右括号是否匹配
*/
function isMatch(left:string,right:string){
if(left==='{' && right === '}') return true
if(left==='[' && right === ']') return true
if(left==='(' && right === ')') return true
return false
}
/**
* 判断括号是否匹配
*/
function matchBracket(str:string): boolean{
const length = str.length
if(length === 0) return true
const stack = []
const leftSymbols = '{[('
const rightSymbols = '}])'
for(let i=0;i<length;i++){
const s = str[i]
if(leftSymbols.includes(s)){
//左括号,压栈
stack.push(s)
}else if(rightSymbols.includes(s)){
//有括号,判断栈顶(是否出栈)
const top = stack[stack.length - 1]
if(isMatch(top,s)){
stack.pop()
}else{
return false
}
}
}
return stack.length === 0
}给一个数组,找出其中和为n的两个元素
有一个递增的数组[1,2,4,7,11,15]和一个n=15,数组中有两个数,和是n。即4+11===15。写出一个函数,找出这两个数。
常规思路是嵌套循环,找到一个数,然后去遍历下一个数,求和,判断。但是时间复杂度是o(n^2),不可用。
function findTowNumbers1(arr:number[],n:number): number[]{
const res: number[] = []
const length = arr.length
if(length === 0) return res
for(let i=0;i<length-1;i++){
const n1 = arr[i]
let flag = false // 是否得到了结果
for(let j =i+1;j<length;j++){
const n2 = arr[j]
if(n1+n2===n){
res.push(n1)
res.push(n2)
flag = true
break
}
}
if(flag) break
}
return res
}如何优化呢?我们可以利用递增(有序)的特性,随便找两个数,如果和大于n,则需要向前寻找,如果和小于n,则需要向后寻找--二分法。
使用双指针,时间复杂度降低到O(n),定义i指向头,j指向尾,求arr[i]+arr[j]
如果大于n,则j需要向前移动,如果小于n,则i需要向后移动
function findTowNumbers1(arr:number[],n:number): number[]{
const res: number[] = []
const length = arr.length
if(length === 0) return res
let i = 0 //头
let j = length -1 //尾
while(i<j){
const n1 = arr[i]
const n2 = arr[j]
const sum = n1 + n2
if(sum>n){
//sum大于n,则j要向前移动
j--
}else if(sum<n){
//sum小于n,则i要向后移动
i++
}else{
//相等
res.push(n1)
res.push(n2)
break
}
}
return res
}用JS实现二分查找,并说明时间复杂度
思路是有两种,一种是递归,代码逻辑更加清晰,二分之一的查找。非递归,性能更好,时间复杂度是O(logn)非常快。
循环查找
function binarySearch1(arr:number[],target:number): number{
const length = arr.length
if(length === 0) return -1
let startIndex = 0 //开始位置
let endIndex = length - 1 //结束位置
while(startIndex<=endIndex){
const midIndex = Math.floor((startIndex + endIndex)/2)
const midValue = arr[midIndex]
if(target < midValue){
//目标值较小,则继续在左侧查找
endIndex = midIndex - 1
}else if(target > midValue){
//目标值较大,则继续在右侧查找
startIndex = midIndex + 1
}else{
//相等,返回
return midIndex
}
}
return -1
}递归查找
function binarySearch2(arr:number[],target:number,startIndex?:number,endIndex?:number): number[]{
const length = arr.length
if(length === 0) return -1
//开始和结束的范围
if(startIndex == null) startIndex = 0
if(endIndex == null) endIndex = length - 1
//如果start和end相遇,则结束
if(startIndex > endIndex) return -1
//中间位置
const midIndex = Math.floor((startIndex + endIndex)/2)
const midValue = arr[midIndex]
if(target<midValue){
//目标值较小,则继续在左侧查找
return binarySearch2(arr,target,startIndex,midIndex - 1)
}else if(target>midValue){
//目标值较大,则继续在右侧查找
return binarySearch2(arr,target,midIndex + 1 , endIndex)
}else{
//相等返回
return midIndex
}
}循环和递归哪个更快呢?循环较快一些,循环就是一个函数,不停地去while循环,但是递归要频繁的调用多次函数,每次调用函数都有开销,因此循环会较快一些。
记住凡有序,必二分。凡二分,时间复杂度必包含O(logn)。
数字千分位格式化
将数字千分位格式化,输出字符串。如输入数字12050100,输出字符串12,050,100
常规思路是转换为数组,reverse,每3位拆分。或者使用正则表达式,又或者使用字符串拆分。
使用数组的方式
function format(n:number):string{
n = Math.floor(n) //只考虑整数的情况
const s = n.toString()
const arr = s.split('').reverse()
return arr.reduce((prev,val,index)=>{
if(index%3===0){
if(prev){
return val + ',' + prev
}else{
return val
}
}else{
return val+prev
}
},'')
}使用字符串分析的方式
function format(n:number):string{
n = Math.floor(n) //只考虑整数的情况
let res = ''
const s = n.toString()
const length = s.length
for(let i = length - 1;i>=0;i--){
const j = length - i
if(j % 3 ===0){
if(i===0){
res = s[i]+res
}else{
res = ','+s[i]+res
}
}else{
res = s[i] + res
}
}
return res
}用JS切换字母大小写
输入一个字符串,切换其中字母的大小写,如输入字符串12aBc34,输出字符串12AbC34。
常见思路有两个一个是正则表达式,另一个是ASCII码判断。
正则表达式方式
function switchLetterCase(s:string): string{
const res = ''
const length = s.length
if(length === 0) return res
const reg1 = /[a-z]/
const reg2 = /[A-Z]/
for(let i = 0;i<length;i++){
const c = s[i]
if(reg1.test(c)){
res += c.toUpperCase()
}else if(reg2.test(c)){
res += c.toLowerCase()
}else{
res += c
}
}
return res
}ASCII码方式
function switchLetterCase(s:string): string{
const res = ''
const length = s.length
if(length === 0) return res
const reg1 = /[a-z]/
const reg2 = /[A-Z]/
for(let i = 0;i<length;i++){
const c = s[i]
const code = c.charCodeAt(0)
if(code>=65&&code<=90){
res += c.toLowerCase()
}else if(code>=97&&code<=122){
res += c.toUpperCase()
}else{
res += c
}
}
return res
}为何0.1+0.2!==0.3
计算机使用二进制存储数据,整数转换二进制没有误差,如9转换为二进制是1001,而小数可能无法用二进制准确表达,如0.2转换为1.1001100...。那转换不过来怎么办呢?我们也只能取其精度,忽略个第几位才行。不光是JS,其他编程语言也是一样的。那么在JS中的执行结果如下: 
如果你经常操作0.1+0.2的小数的话,你可以使用第三方库,https://www.npmjs.com/package/mathjs
